第7章のPythonコード

第7章 外生変数と内生変数

モジュールのインポート

import numpy as np
import pandas as pd
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib

Rによるシミュレーション演習

乱数の設定

np.random.seed(2022)

サンプルサイズとパラメータの設定

n  = 200 # サンプルサイズ
b0 = 1   # 切片の真の値
b1 = 2   # 係数の真の値

estimate()関数の定義

def estimate(lambda2) :
  e = np.random.normal(size = n)                         # 誤差項
  X = (1 + lambda2 * e) * np.random.uniform(size = n)    # 説明変数
  Y = b0 + b1 * X + e                                    # 被説明変数
  mydata = pd.DataFrame(np.array([X, Y]).transpose(), columns = ['X', 'Y'])
  regression = ols('Y ~ X', data = mydata).fit()
  return regression.params

simulate()関数の定義

def simulate(lambda2) :
  betahat0 = np.zeros(100)
  betahat1 = np.zeros(100)

  for i in range(100) :
    betahat0[i] = estimate(lambda2)[0]
    betahat1[i] = estimate(lambda2)[1]
  
  mean0 = pd.DataFrame(betahat0).mean()
  mean1 = pd.DataFrame(betahat1).mean()

  mydata = pd.DataFrame(np.array([mean0, mean1]).transpose(), columns = ['beta0', 'beta1'])

  return mydata

シミュレーションの実施

results = pd.DataFrame(columns = ['beta0', 'beta1'])
lambdas = np.linspace(0, 0.6, 61)
for i in map(simulate, lambdas) :
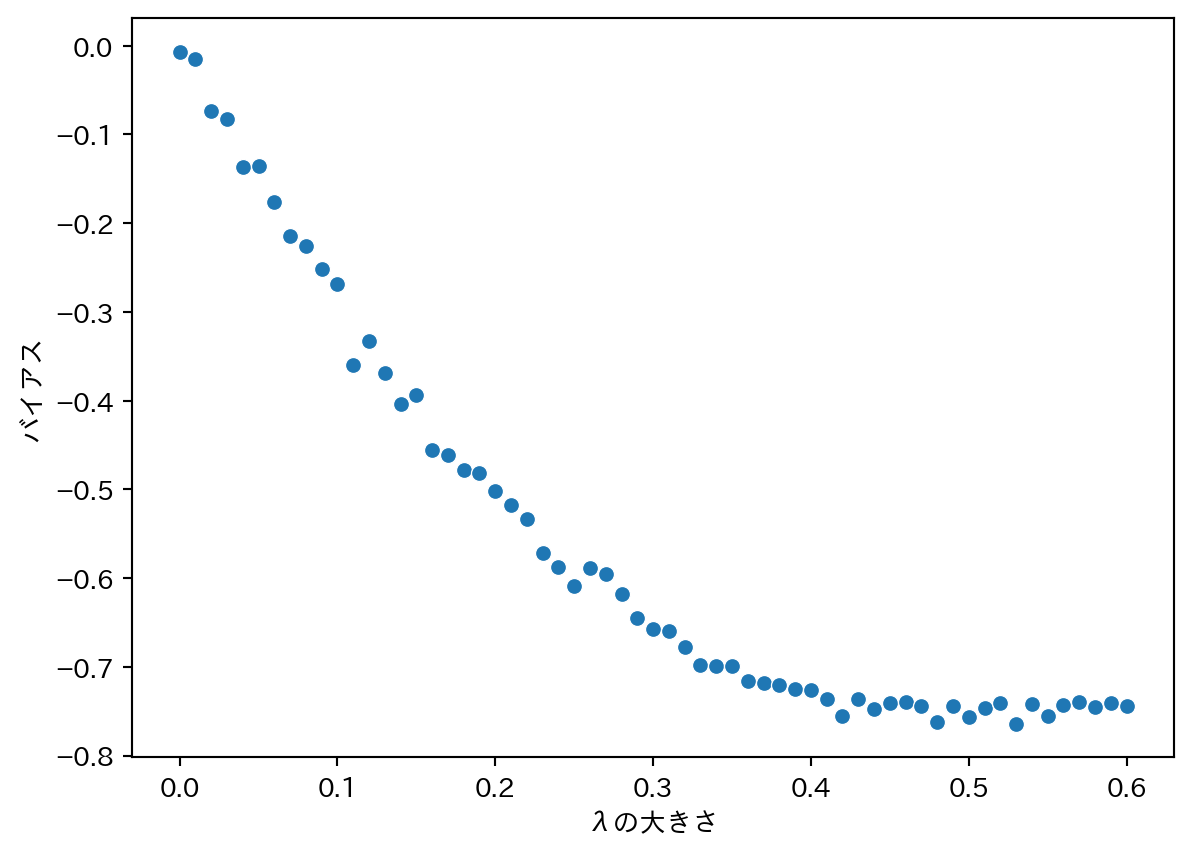
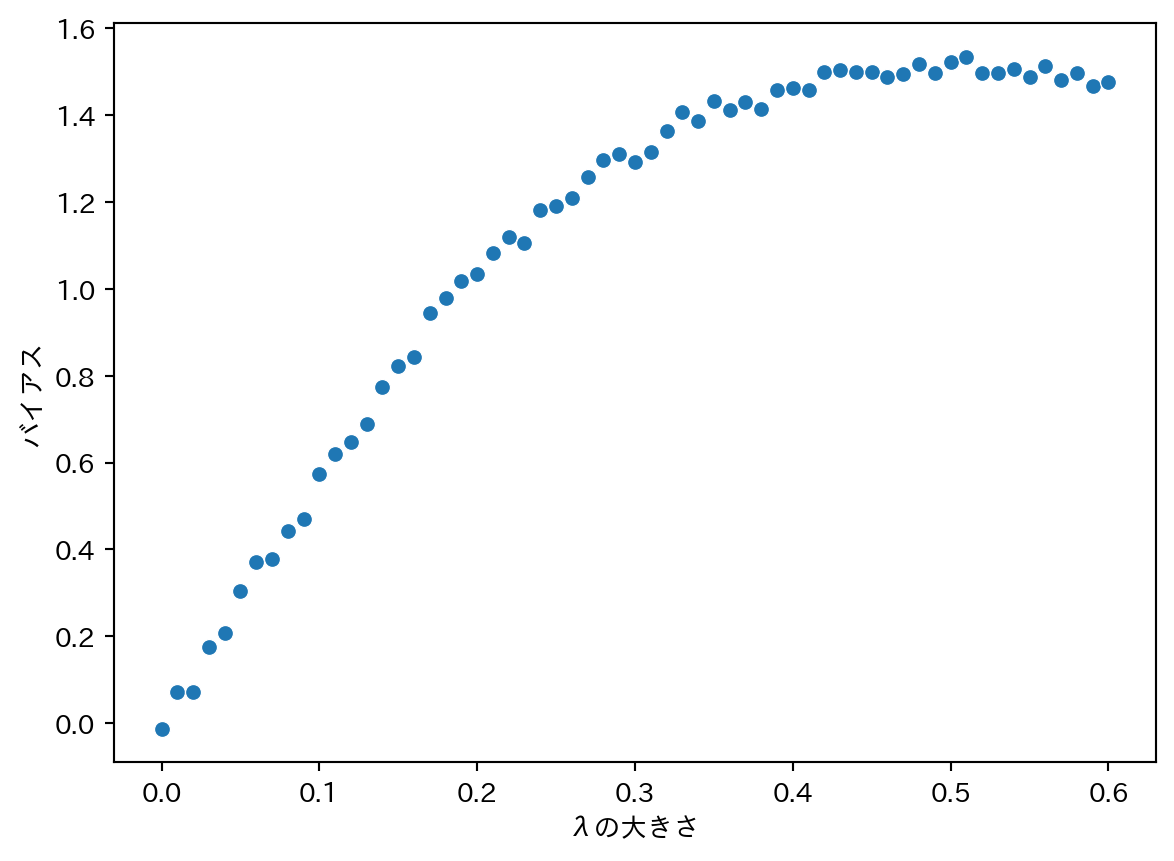
  results = pd.concat([results, i], ignore_index = True)
results['bias0'] =  results['beta0'] - b0 # バイアス = 推定値 - 真の値
results['bias1'] =  results['beta1'] - b1
results['lambdas'] = lambdas