第5章のPythonコード

第5章 推測統計の基礎

サンプルデータ

distributions.csv：異なる分布のシミュレーションデータ．

wage.csv：1976年の米国における男性労働者の賃金に関するデータ．

temperature_aug.csv：2014年8月の東京都の気温データ．

モジュールのインポート

import numpy as np
from scipy.stats import binom
import pandas as pd
from scipy.stats import norm
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt

5.1 統計的仮説検定の考え方

5.1.3 コイン投げの例

p40 = binom.cdf(k = 40, n = 100, p = 0.5)
p60 = binom.cdf(k = 60, n = 100, p = 0.5)

print(p60 - p40)
0.9539559330706573

5.2 平均値の検定

5.2.5 Rによる例題演習

simdata = pd.read_csv('distributions.csv')

sample_mean = simdata.mean(numeric_only = True)[0]
sample_var = simdata.var(numeric_only = True)[0]

print(
    "Mean of A: ", sample_mean, "\n",
    "Varicane of A: ", sample_var, "\n",
    "t-value: ", (100 ** 0.5) * (sample_var ** -0.5) * (sample_mean)
)
Mean of A:  2.0423230835000004 
 Varicane of A:  0.37278460765476673 
 t-value:  33.44994900706078

5.2.6 \(p\)値

1 - norm.cdf(x = 1.250113) +  norm.cdf(x = -1.250113)
0.21125827155567078

5.3 回帰係数の検定

5.3.2 \(\hat{\beta}_1\)の分布のシミュレーション

np.random.seed(2022)

X = np.random.normal(loc = 0, scale = 1, size = 1000)
Y = 1 + 5 * X + np.random.normal(loc = 0, scale = 1, size = 1000)

mydata = pd.DataFrame(np.array([X, Y]).transpose(), columns = ['X', 'Y'])

beta1 = ols('Y ~ X', data = mydata).fit().params[1]
S = 10000
beta1 = np.zeros(S) # 結果の保存
for i in range(S):      # 繰り返し開始
  X = np.random.normal(loc = 0, scale = 1, size = 1000)
  Y = 1 + 5 * X + np.random.normal(loc = 0, scale = 1, size = 1000)
  mydata = pd.DataFrame(np.array([X, Y]).transpose(), columns = ['X', 'Y'])
  beta1[i] = ols('Y ~ X', data = mydata).fit().params[1]
  # 繰り返し終了
pd.DataFrame(beta1).describe()
0
count 10000.000000
mean 5.000060
std 0.031486
min 4.887715
25% 4.978288
50% 4.999855
75% 5.021525
max 5.120464 
plt.hist(beta1, bins = 20)
plt.show()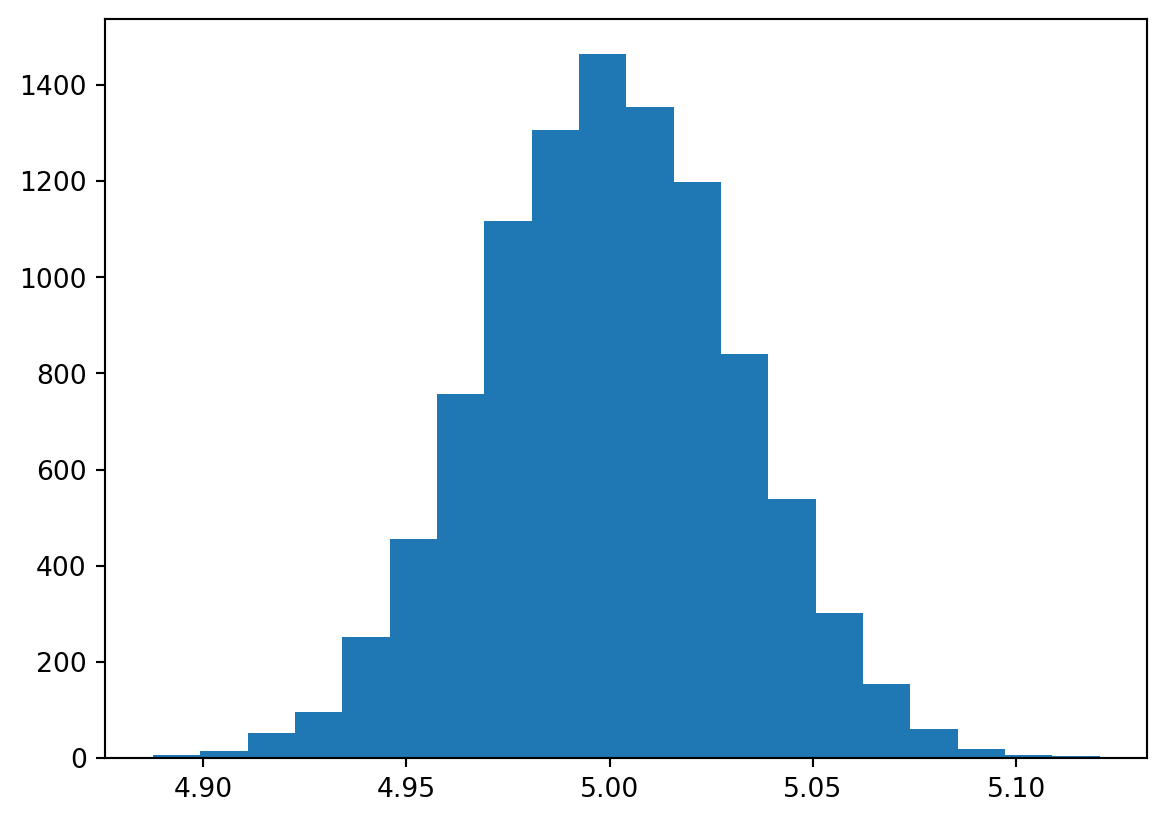

5.3.6 Rによる分析例

wagedata = pd.read_csv('wage.csv')

wagedata['log_wage'] = np.log(wagedata['wage'])

result = ols('log_wage ~ educ + exper', data = wagedata).fit()
print(result.summary())
                            OLS Regression Results                            
==============================================================================
Dep. Variable:               log_wage   R-squared:                       0.181
Model:                            OLS   Adj. R-squared:                  0.181
Method:                 Least Squares   F-statistic:                     333.0
Date:                Wed, 05 Jun 2024   Prob (F-statistic):          2.32e-131
Time:                        18:21:20   Log-Likelihood:                -1524.1
No. Observations:                3010   AIC:                             3054.
Df Residuals:                    3007   BIC:                             3072.
Df Model:                           2                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      4.6660      0.064     73.147      0.000       4.541       4.791
educ           0.0932      0.004     25.796      0.000       0.086       0.100
exper          0.0407      0.002     17.417      0.000       0.036       0.045
==============================================================================
Omnibus:                       37.191   Durbin-Watson:                   1.739
Prob(Omnibus):                  0.000   Jarque-Bera (JB):               41.243
Skew:                          -0.228   Prob(JB):                     1.11e-09
Kurtosis:                       3.348   Cond. No.                         140.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
print(0.0932 / 0.004)
23.3

5.4 信頼区間

5.4.2 Rによる分析例

result = ols('log_wage ~ educ + exper', data = wagedata).fit()

print(result.summary())
                            OLS Regression Results                            
==============================================================================
Dep. Variable:               log_wage   R-squared:                       0.181
Model:                            OLS   Adj. R-squared:                  0.181
Method:                 Least Squares   F-statistic:                     333.0
Date:                Wed, 05 Jun 2024   Prob (F-statistic):          2.32e-131
Time:                        18:21:20   Log-Likelihood:                -1524.1
No. Observations:                3010   AIC:                             3054.
Df Residuals:                    3007   BIC:                             3072.
Df Model:                           2                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      4.6660      0.064     73.147      0.000       4.541       4.791
educ           0.0932      0.004     25.796      0.000       0.086       0.100
exper          0.0407      0.002     17.417      0.000       0.036       0.045
==============================================================================
Omnibus:                       37.191   Durbin-Watson:                   1.739
Prob(Omnibus):                  0.000   Jarque-Bera (JB):               41.243
Skew:                          -0.228   Prob(JB):                     1.11e-09
Kurtosis:                       3.348   Cond. No.                         140.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
betahat = result.params
sigma = result.bse

lower = betahat - 1.96 * sigma
upper = betahat + 1.96 * sigma
pd.concat([lower, upper], axis = 1)
0 1
Intercept 4.541006 4.791063
educ 0.086089 0.100247
exper 0.036082 0.045233 
result.conf_int(alpha = 0.05)
0 1
Intercept 4.540958 4.791111
educ 0.086086 0.100250
exper 0.036080 0.045235 
result.conf_int(alpha = 0.01)
0 1
Intercept 4.501618 4.830451
educ 0.083859 0.102477
exper 0.034641 0.046674