第6章のPythonコード

第6章 相関関係と因果関係

サンプルデータ

video_game.csv：ビデオゲームのプレイ時間と学業成績の架空データ．

police_crime.csv：2014年における都道府県別の警察官の数と犯罪認知件数に関するデータ．

モジュールのインポート

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

6.1 相関 \(\neq\) 因果

videodata = pd.read_csv('video_game.csv')

sns.set_theme()
sns.scatterplot(x = 'hours', y = 'grade', data = videodata)
plt.show()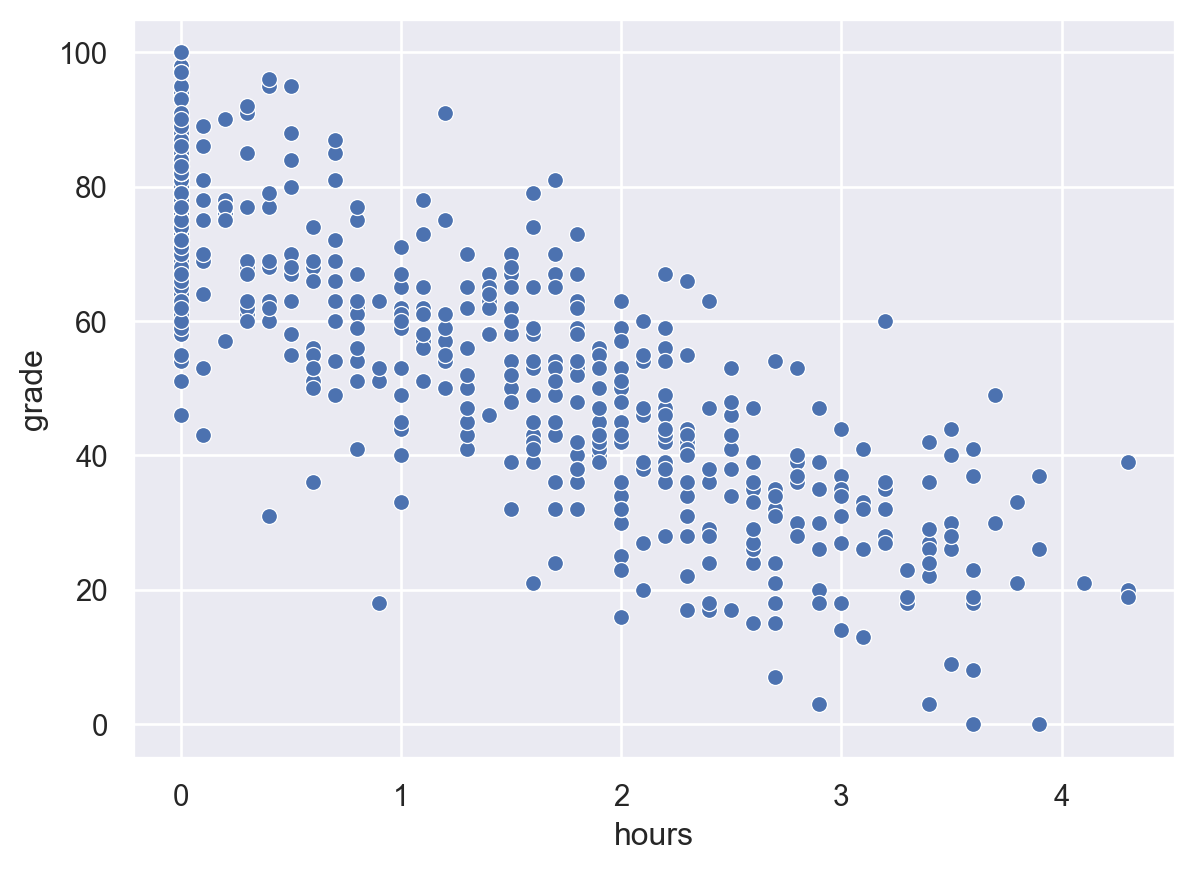

videodata.corr(numeric_only = True)
grade hours
grade 1.000000 -0.820747
hours -0.820747 1.000000

6.1.3 同時性

crimedata = pd.read_csv('police_crime.csv', encoding="shift-jis")

sns.scatterplot(x = 'police', y = 'crime', data = crimedata)
plt.show()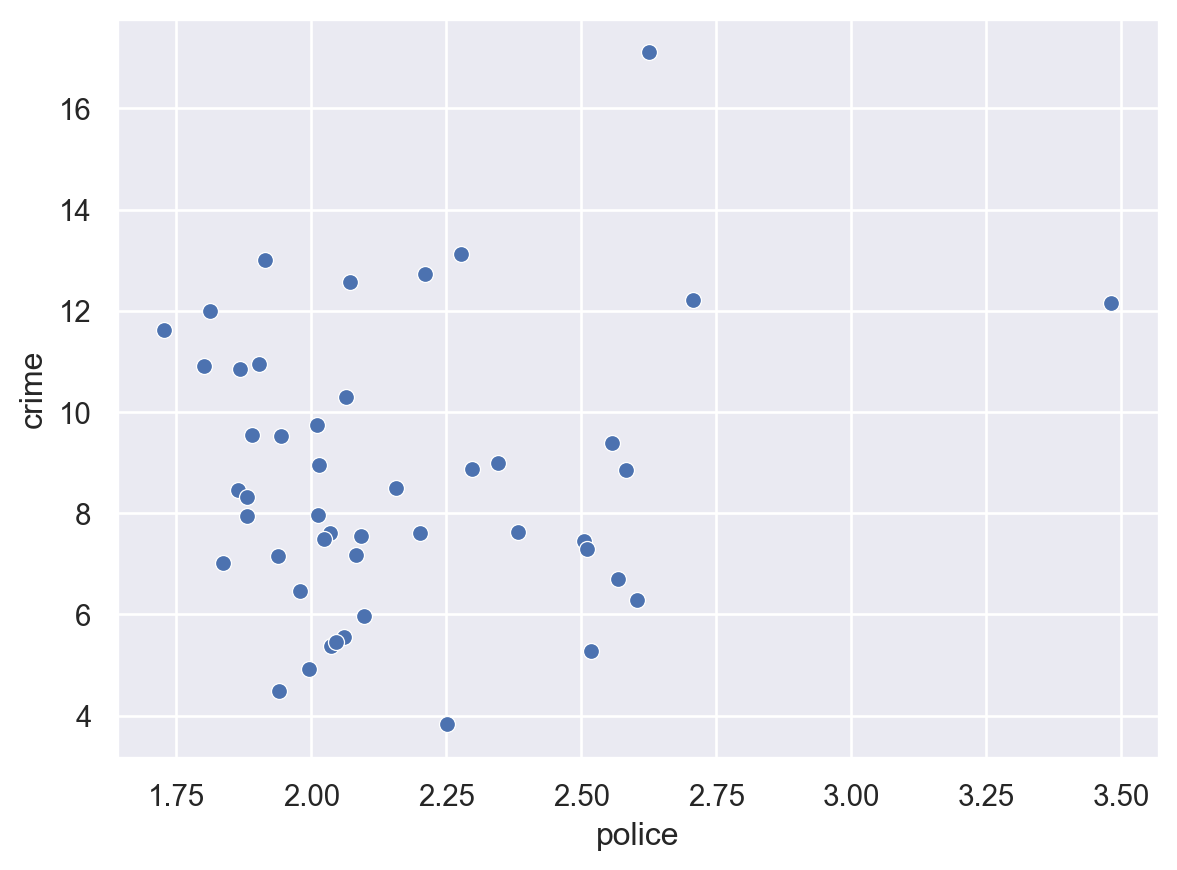

crimedata.corr(numeric_only = True)
police crime
police 1.000000 0.128985
crime 0.128985 1.000000

6.2 ルービンの因果モデル

6.2.2 平均トリートメント効果

np.random.seed(2022)

n = 400
D = np.random.binomial(n = 1, p = 0.6, size = n) # 確率 0.6 で 1，確率 0.4 で 0 をとるトリートメント変数
TE = 2                                           # トリートメント効果 = 2 で個人間の差は無いと想定
Y = TE * D + np.random.normal(size = n)          # 結果変数

EY1 = sum(D * Y) / sum(D)
EY0 = sum((1 - D) * Y) / sum(1 - D)
print(EY1 - EY0)
1.8626205381054488
Z = np.random.uniform(size = n)
D = np.random.binomial(n = 1, p = Z, size = n)
Y = TE * D + (2 * Z - 1) + np.random.normal(size = n)

EY1 = sum(D * Y) / sum(D)
EY0 = sum((1 - D) * Y) / sum(1 - D)
print(EY1 - EY0)
2.707623608936378