import numpy as np
import math
import matplotlib.pyplot as plt
import pandas as pd
import scipy.stats as stats
import seaborn as sns第3章のPythonコード
第3章 確率論の基礎
モジュールのインポート
乱数の設定
np.random.seed(seed = 2022)3.1.2 試行と事象
coin = ['Head', 'Tail']
np.random.choice(coin, size = 100, replace = True)array(['Tail', 'Head', 'Tail', 'Head', 'Tail', 'Tail', 'Head', 'Tail',
'Head', 'Head', 'Head', 'Head', 'Tail', 'Tail', 'Tail', 'Tail',
'Tail', 'Tail', 'Head', 'Head', 'Head', 'Tail', 'Head', 'Tail',
'Head', 'Head', 'Head', 'Tail', 'Head', 'Head', 'Head', 'Tail',
'Head', 'Tail', 'Head', 'Head', 'Tail', 'Tail', 'Tail', 'Tail',
'Tail', 'Tail', 'Tail', 'Tail', 'Head', 'Head', 'Head', 'Head',
'Head', 'Tail', 'Head', 'Tail', 'Tail', 'Head', 'Head', 'Head',
'Head', 'Tail', 'Tail', 'Head', 'Head', 'Tail', 'Head', 'Tail',
'Tail', 'Tail', 'Tail', 'Tail', 'Tail', 'Tail', 'Head', 'Tail',
'Tail', 'Tail', 'Head', 'Head', 'Head', 'Head', 'Tail', 'Head',
'Head', 'Tail', 'Head', 'Tail', 'Tail', 'Head', 'Head', 'Tail',
'Tail', 'Tail', 'Tail', 'Head', 'Tail', 'Tail', 'Tail', 'Tail',
'Head', 'Tail', 'Tail', 'Head'], dtype='<U4')3.1.3 コイン投げのシミュレーション
math.factorial(100) / (math.factorial(50) ** 2) / (2 ** 100)0.07958923738717877coin = [1, 0]
z = np.random.choice(coin, size = 100, replace = True)
z.sum()53S = 100000
rec = np.zeros(S)
coin = [1, 0]
for i in range(S):
z = np.random.choice(coin, 100, replace = True)
rec[i] = z.sum()plt.hist(rec, bins = 20)
plt.show()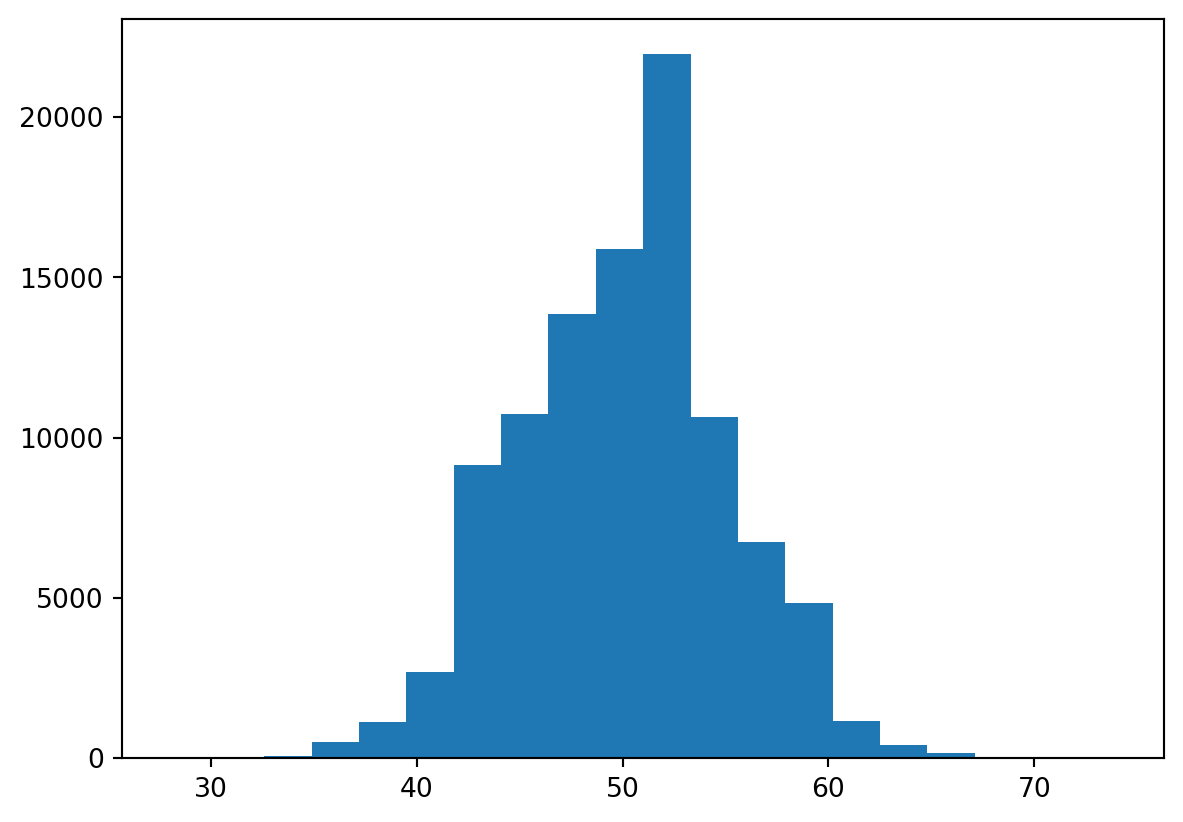
pd.DataFrame(rec).describe()| 0 | |
|---|---|
| count | 100000.000000 |
| mean | 49.986290 |
| std | 4.987395 |
| min | 28.000000 |
| 25% | 47.000000 |
| 50% | 50.000000 |
| 75% | 53.000000 |
| max | 74.000000 |
3.1.4 論理演算によるカウントの方法
2 > 1True2 > 1000False200 == 100 * 2TrueTrue + True2True * False0count = (rec == 50)
print(count)[False False False ... False False False]count.sum()7997count.mean()0.079973.2.3 独立ではない例
# 独立性の確認
S = 10000 # シミュレーション回数
X = np.random.normal(loc = 50, scale = 10, size = S) # Xを抽出
Y = np.random.normal(loc = 50, scale = 10, size = S) # Yを抽出
Z = X + Y # Zを構成# Pr(X > 70) * Pr(Z > 100)
(X > 70).mean() * (Z > 100).mean() 0.010649170000000001# Pr(X > 70 かつ Z > 100)
((X > 70) * (Z > 100)).mean() 0.02073.2.4 独立性と相関係数
X = np.random.normal(loc = 50, scale = 10, size = 100000)
Y = np.random.normal(loc = 50, scale = 10, size = 100000)
np.corrcoef(X, Y)array([[ 1. , -0.0090849],
[-0.0090849, 1. ]])Z = -((X - 50) ** 2) / 10
np.corrcoef(X, Z)array([[1. , 0.00952884],
[0.00952884, 1. ]])plt.scatter(X, Z)
plt.show()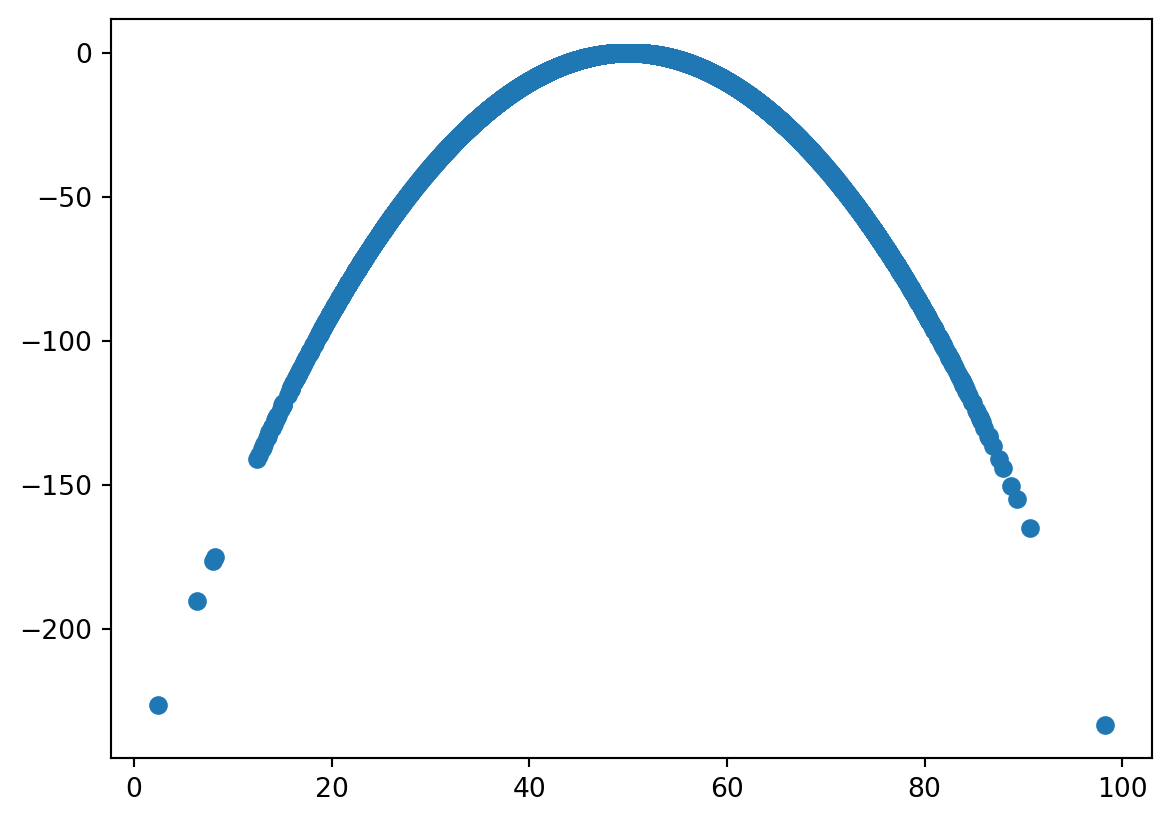
3.3.1 分布関数
x = np.linspace(0, 100, 1000)
plt.plot(x, stats.norm.cdf(x, 50, 10))
plt.show()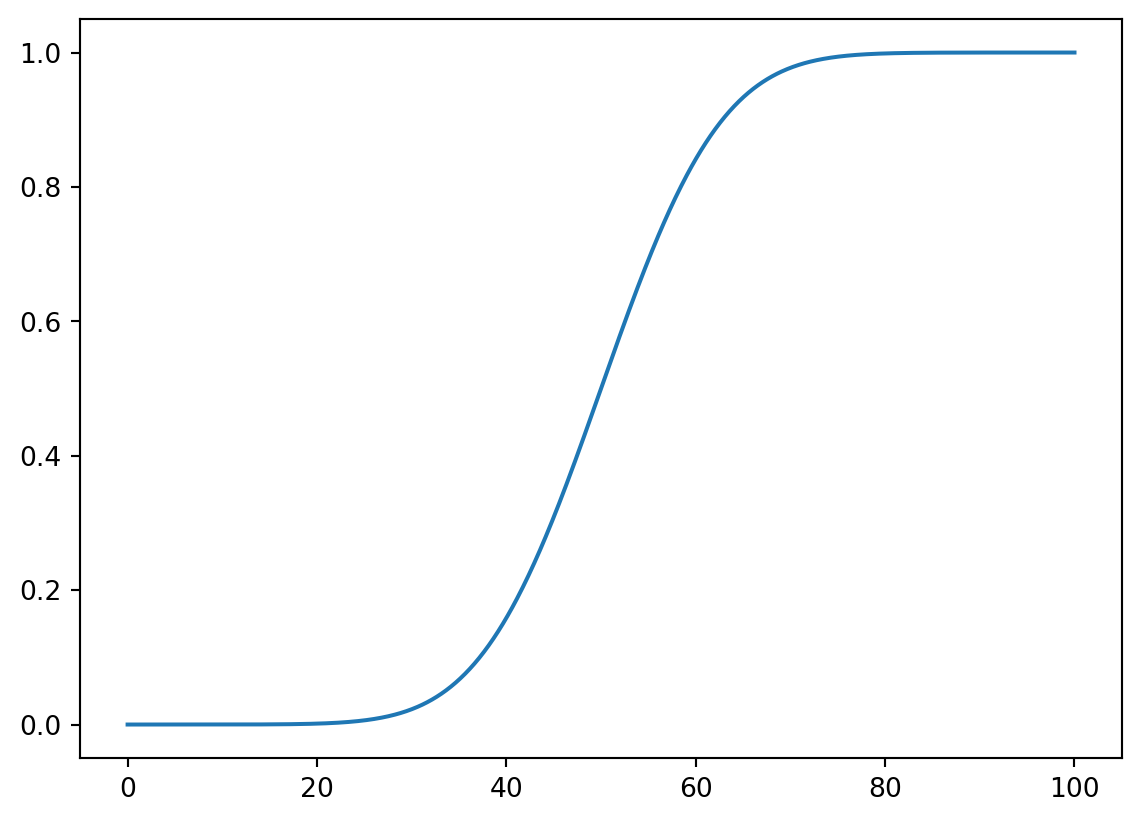
print(stats.norm.cdf(60, 50, 10) - stats.norm.cdf(40, 50, 10))0.68268949213708593.3.2 確率密度関数
print(stats.norm.cdf(50 + 0.1, 50, 10) - stats.norm.cdf(50, 50, 10))0.003989356314631709print(stats.norm.pdf(50, 50, 10))0.03989422804014327print(stats.norm.pdf(80, 50, 10))0.00044318484119380076x = np.linspace(start = 0, stop = 100, num = 1000)
plt.plot(x, stats.norm.pdf(x, 50, 10))
plt.show()3.3.7 データによる条件付期待値の推定
wagedata = pd.read_csv("wage.csv")
wagedata.head()| educ | exper | wage | |
|---|---|---|---|
| 0 | 7 | 16 | 548.000002 |
| 1 | 12 | 9 | 481.000000 |
| 2 | 12 | 16 | 721.000002 |
| 3 | 11 | 10 | 250.000001 |
| 4 | 12 | 16 | 728.999999 |
wagedata.describe()| educ | exper | wage | |
|---|---|---|---|
| count | 3010.000000 | 3010.000000 | 3010.000000 |
| mean | 13.263455 | 8.856146 | 577.282392 |
| std | 2.676913 | 4.141672 | 262.958303 |
| min | 1.000000 | 0.000000 | 100.000000 |
| 25% | 12.000000 | 6.000000 | 394.250000 |
| 50% | 13.000000 | 8.000000 | 537.499999 |
| 75% | 16.000000 | 11.000000 | 708.750001 |
| max | 18.000000 | 23.000000 | 2404.000010 |
sns.pairplot(wagedata)<seaborn.axisgrid.PairGrid at 0x12592fa90>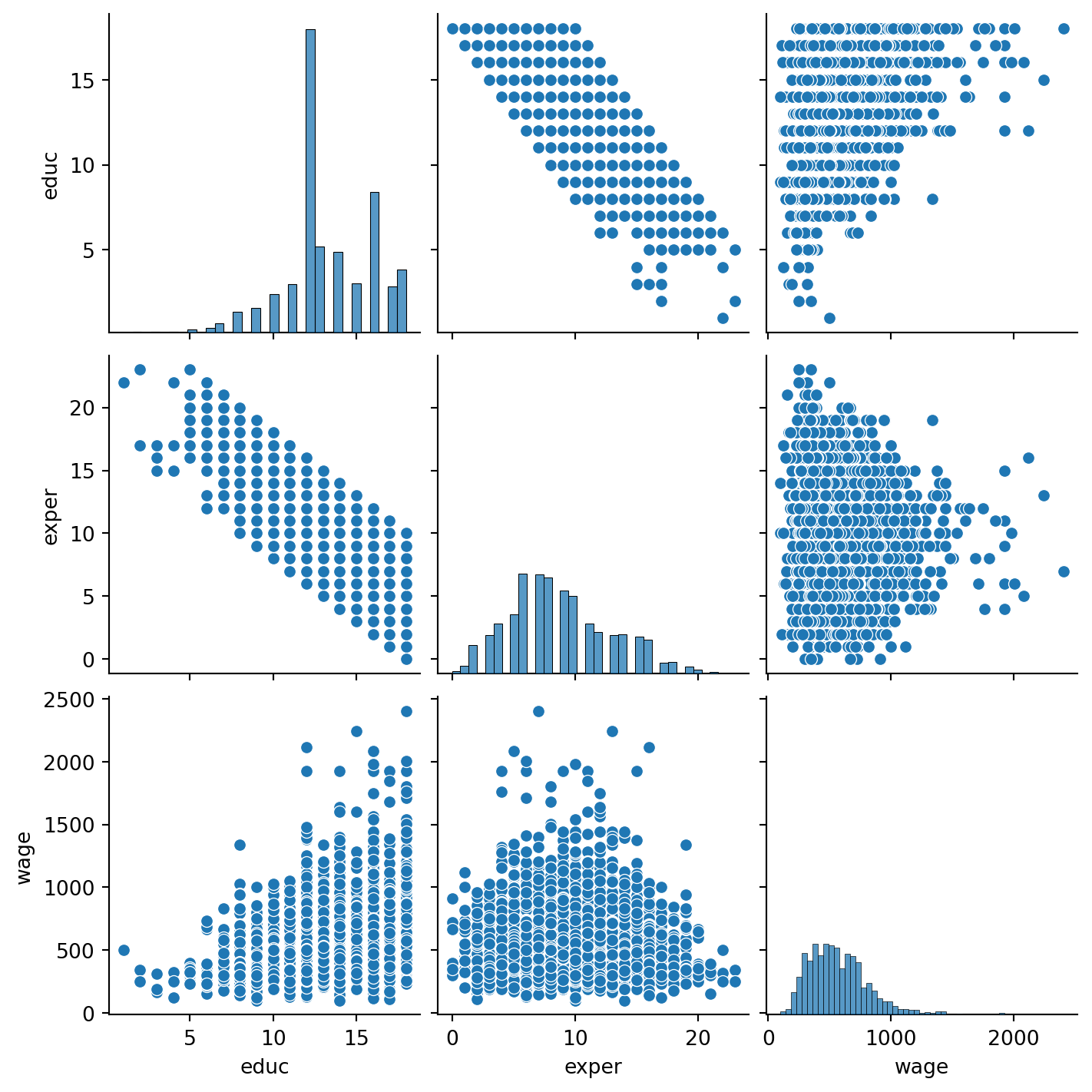
educ12 = wagedata.loc[wagedata['educ'] == 12]
educ16 = wagedata.loc[wagedata['educ'] == 16]educ12['wage'].mean()563.5342744186569educ16['wage'].mean()642.8932464464075educ11_less = wagedata.loc[wagedata['educ'] < 12]
educ12_more = wagedata.loc[wagedata['educ'] >= 12]
educ11_less['wage'].mean()438.10865197516847educ12_more['wage'].mean()604.80700384708583.4.2 中心極限定理のシミュレーション
S = 10000
n = 10000
Zn = np.zeros(S)
for i in range(S):
X = np.random.normal(loc = 50, scale = 10, size = n)
Xbar = X.mean()
Sn = X.var()
Zn[i] = (n ** 0.5) * (Xbar - 50) / (Sn ** 0.5)
plt.hist(Zn, bins = 20)
plt.show()
pd.DataFrame(Zn).describe()| 0 | |
|---|---|
| count | 10000.000000 |
| mean | 0.010709 |
| std | 1.000739 |
| min | -3.803410 |
| 25% | -0.663426 |
| 50% | 0.015367 |
| 75% | 0.688068 |
| max | 3.487146 |
3.4.3 信頼区間のシミュレーション
# 信頼区間シミュレーション
S = 10000 # シミュレーション回数
n = 10000 # 標本の大きさ
rec = np.zeros(S) # 結果記録用のベクトル
for i in range(S): # 繰り返し開始
X = np.random.normal(loc = 50, scale = 10, size = n) # N(50,10^2) から標本抽出
Xbar = X.mean()
Sn = X.var()
rec[i] = (Xbar - 1.96 * ((Sn / n) ** 0.5) < 50) * (50 < Xbar + 1.96 * ((Sn / n) ** 0.5))
rec.mean() # 確率を計算0.94663.4.4 信頼区間の導出
print(stats.norm.cdf(69.6, 50, 10) - stats.norm.cdf(30.4, 50, 10))0.9500042097035591