第5章のStataコード

第5章 推測統計の基礎

サンプルデータ

distributions.csv：異なる分布のシミュレーションデータ．

wage.csv：1976年の米国における男性労働者の賃金に関するデータ．

temperature_aug.csv：2014年8月の東京都の気温データ．

5.1 統計的仮説検定の考え方

5.1.3 コイン投げの例

clear
display binomial(100, 60, 0.5) - binomial(100, 40, 0.5)
.95395593

5.2 平均値の検定

5.2.5 Rによる例題演習

import delimited "distributions.csv", clear
summarize dista, detail
                            distA
-------------------------------------------------------------
      Percentiles      Smallest
 1%     1.005143        1.00268
 5%     1.071364       1.007606
10%     1.242875       1.027831       Obs                 100
25%     1.436728       1.061649       Sum of wgt.         100

50%     2.139604                      Mean           2.042323
                        Largest       Std. dev.      .6105609
75%     2.566881       2.906963
90%     2.839471       2.909304       Variance       .3727846
95%     2.889779       2.940179       Skewness      -.1250327
99%     2.947699        2.95522       Kurtosis       1.643932
display sqrt(100) / sqrt(r(Var)) * r(mean)
33.449949

5.2.6 \(p\)値

display 1 - normal(1.250113) + normal(-1.250113)
.21125827

5.3 回帰係数の検定

5.3.2 \(\hat{\beta}_1\)の分布のシミュレーション

clear
set seed 2022

postfile sim beta1 using betahats1000, replace

forvalues i = 1/10000 {
    quietly capture drop X Y
    quietly set obs 100
    quietly generate X = rnormal(0, 1)
    quietly generate Y = 1 + 5 * X + rnormal(0, 1)
    quietly regress Y X
    post sim (e(b)[1, 1])
}

postclose sim
use betahats1000, clear
summarize beta1
                            beta1
-------------------------------------------------------------
      Percentiles      Smallest
 1%     4.924835       4.876307
 5%      4.94757        4.88193
10%     4.959229       4.882976       Obs              10,000
25%     4.978507       4.887352       Sum of wgt.      10,000

50%     5.000195                      Mean           4.999877
                        Largest       Std. dev.      .0320337
75%     5.021528       5.115664
90%     5.040558       5.115983       Variance       .0010262
95%     5.051876       5.117807       Skewness      -.0005134
99%     5.074158       5.122896       Kurtosis       3.105771
histogram beta1, frequency bin(12)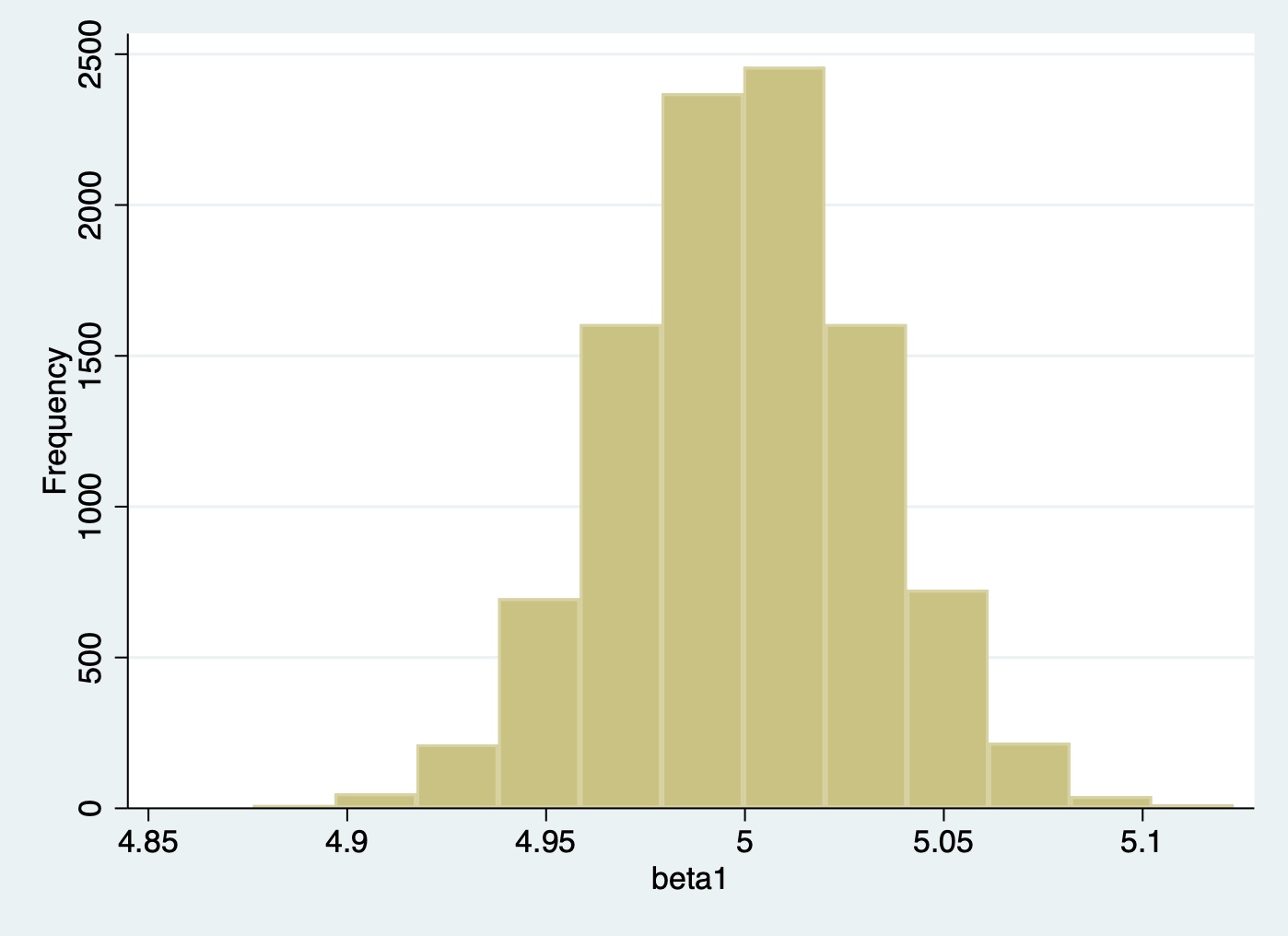

5.3.6 Rによる分析例

import delimited "wage.csv", clear
regress wage educ exper
      Source |       SS           df       MS      Number of obs   =     3,010
-------------+----------------------------------   F(2, 3007)      =    332.48
       Model |    37678267         2  18839133.5   Prob > F        =    0.0000
    Residual |   170385263     3,007  56662.8743   R-squared       =    0.1811
-------------+----------------------------------   Adj R-squared   =    0.1805
       Total |   208063530     3,009  69147.0688   Root MSE        =    238.04

------------------------------------------------------------------------------
        wage | Coefficient  Std. err.      t    P>|t|     [95% conf. interval]
-------------+----------------------------------------------------------------
        educ |   55.05451   2.140332    25.72   0.000     50.85785    59.25118
       exper |   25.14156   1.383374    18.17   0.000     22.42911    27.85402
       _cons |   -375.588   37.80211    -9.94   0.000    -449.7087   -301.4674
------------------------------------------------------------------------------
display (55.05451 / 2.140332)
25.722416

5.4 信頼区間

5.4.2 Rによる分析例

regress wage educ exper
      Source |       SS           df       MS      Number of obs   =     3,010
-------------+----------------------------------   F(2, 3007)      =    332.48
       Model |    37678267         2  18839133.5   Prob > F        =    0.0000
    Residual |   170385263     3,007  56662.8743   R-squared       =    0.1811
-------------+----------------------------------   Adj R-squared   =    0.1805
       Total |   208063530     3,009  69147.0688   Root MSE        =    238.04

------------------------------------------------------------------------------
        wage | Coefficient  Std. err.      t    P>|t|     [95% conf. interval]
-------------+----------------------------------------------------------------
        educ |   55.05451   2.140332    25.72   0.000     50.85785    59.25118
       exper |   25.14156   1.383374    18.17   0.000     22.42911    27.85402
       _cons |   -375.588   37.80211    -9.94   0.000    -449.7087   -301.4674
------------------------------------------------------------------------------
regress wage educ exper, level(99)
      Source |       SS           df       MS      Number of obs   =     3,010
-------------+----------------------------------   F(2, 3007)      =    332.48
       Model |    37678267         2  18839133.5   Prob > F        =    0.0000
    Residual |   170385263     3,007  56662.8743   R-squared       =    0.1811
-------------+----------------------------------   Adj R-squared   =    0.1805
       Total |   208063530     3,009  69147.0688   Root MSE        =    238.04

------------------------------------------------------------------------------
        wage | Coefficient  Std. err.      t    P>|t|     [99% conf. interval]
-------------+----------------------------------------------------------------
        educ |   55.05451   2.140332    25.72   0.000     49.53788    60.57115
       exper |   25.14156   1.383374    18.17   0.000     21.57596    28.70716
       _cons |   -375.588   37.80211    -9.94   0.000    -473.0217   -278.1544
------------------------------------------------------------------------------